algebra

Borderline irresponsible discussion of math below. If you are a math friend reading this lmk your thoughts.

With all this "rings" stuff, I have been thinking about algebraic rings, too. Denoted as $< R, +, \cdot >$ .

Quick intro is they are defined as a set with two binary operators, addition ( $+$ ) and multiplication ( $\cdot$ ), where the following axioms hold:

$< R, + >$ is an abelian group (a.k.a. commutative group), meaning:
1. $(a + b) + c = a + (b + c)$ , i.e. addition is associative
2. $a + b = b + a$ , i.e. addition is commutative
3. There exists an element $e$ in $R$ such that $a + e = a$ ( $R$ contains an identity element)
4. For every $a$ in $R$ , there exists an $a^{'}$ such that $a + a^{'} = e$ (all elements have an inverse)
Multiplication is associative, i.e. $(a \cdot b) \cdot c = a \cdot (b \cdot c)$ .
For all $a, b, c$ in $R$ , the left distributive law, $a \cdot (b + c) = (a \cdot b) + (a \cdot c)$ and the right distributive law $(a + b) \cdot c = (a \cdot c) + (b \cdot c)$ hold.

Frankly, I was decent at Modern Algebra I but really bad at Modern Algebra II (one indicator of how my brain function deteriorated from epilepsy, tbh). So don't reeeally take me at my word here.

Thinking about structuring this site as an algebraic ring is not possible as far as I am aware. While the inverse of a blog post might be a thing you could figure out, what would multiplying texts mean, and then what is the "identity text." How could you possibly distribute a text (i meant in a math way, but I guess I am already distributing this text, hmmmmmmm).

Idk, mostly I wanted to write the above to see how the math formatting holds up in the garden, and it was fun.

Groups might be approachable though!

Note

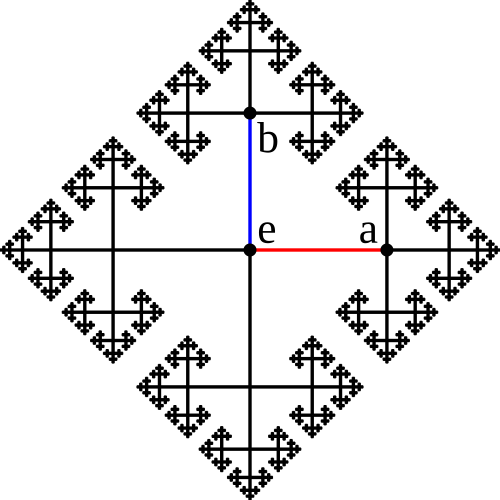
This image of a Cayley graph of the free group on two generators is reminiscent of this site's structure but it's absolutely not the same at all in any ways. But it's pretty! And I am not quite sure what the free group is, I think I learned abt it but don't remember anything about it.

The graph of some parts of this website sorta remind me of cyclic groups and their cycle graphs! Cyclic groups were one of the only things I was able to wrap my head around in Algebra II, and I really like them. Could think about this.

Dihedral groups are another thing I liked in algebra. And are even more approachable for making a gardening of this form at some point.

Note

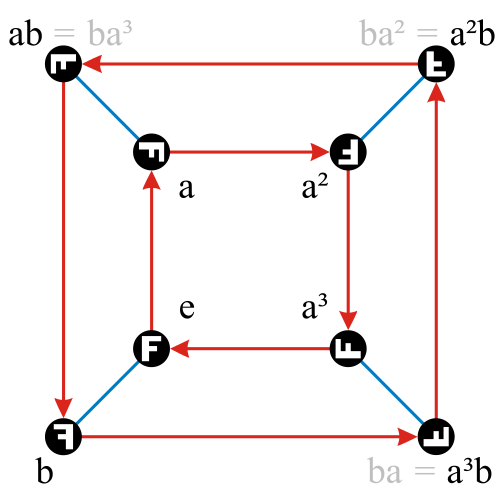
Dih_4_Cayley_Graph;_generators_a,_b.png
Cayley graph of $D_{4}$ (dihedral group of order 4, a.k.a. symmetries of a square) on two generators ( $a$ is a rotation, $b$ is a reflection) got me thinking...

Aaaanyways, thinking fuzzily. If any math friends read this let me know if you have any bright ideas.

Note

Some of these depictions of cycle graphs got me thinking too...

While I'm talking about groups, shoutout to my favorite frieze groups, which I gave a presentation on shortly after John Conway died and it made my professor cry. Groups you can dance to, as he described.

Note

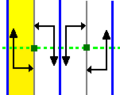
The "spinning sidle" frieze group is a good one to leave in the snow that is on the ground right now, but be careful.

algebra

Thoughts Gardening

previous page ⇽ 💬 ⇾ next page